I sistemi di drenaggio rappresentano una delle tecniche più efficaci per la stabilizzazione dei pendii, in quanto agiscono simultaneamente sulla riduzione delle forze destabilizzanti e sull’incremento della resisteza del terreno. Tra le diverse soluzioni adottabili rientrano trincee drenanti, pozzi, gallerie e dreni tubolari. In alcuni casi, quando non è possibile garantire il deflusso per gravità, si ricorre all’uso di pompe, anche con dispositivi di attivazione automatica, per l’emungimento di acque profonde o per la gestione di configurazioni particolarmente complesse.
La scelta del sistema più idoneo dipende dalla profondità della superficie di scorrimento, dalla morfologia del versante e dalla presenza di eventuali opere esistenti nel campo di intervento.
L’efficacia di un drenaggio non dipende direttamente dalla quantità d’acqua estratta, ma dalla sua capacità di modificare il regime delle pressioni interstiziali. Tuttavia, tale modifica induce fenomeni di consolidazione differenziale che possono causare cedimenti, i quali potrebbero interferire con le opere presenti nell’area instabile. È quindi fondamentale considerare non solo i benefici in termini di stabilità, ma anche i potenziali impatti collaterali.
La progettazione delle opere di drenaggio, indipendentemente dalla tipologia adottata, è spesso affrontata con un approccio empirico, dovuto alla difficoltà di definire modelli affidabili. Quando possibile, si ricorre a modellazioni numeriche avanzate per simulare diversi scenari e migliorare la previsione degli effetti del drenaggio. Tuttavia, la necessità di dati precisi e la complessità dei modelli ne limitano la diffusione. Per questa ragione, è comune affidarsi alla progettazione osservazionale, che prevede il monitoraggio in situ e l’adattamento progressivo dell’intervento. Questa strategia, però, presenta criticità: tempi lunghi, costi incerti nelle fasi iniziali e minore rapidità d’esecuzione.
Di conseguenza, una progettazione efficace richiede un equilibrio tra metodo empirico, osservazione sul campo e strumenti di calcolo, per ridurre le incertezze e migliorare l’efficacia degli interventi.
Nel seguito dell’articolo si illustrano i concetti fondamentali utilizzati nella progettazione di massima delle trincee drenanti, facendo riferimento al lavoro di Desideri, Miliziano e Rampello [1].
Indicazioni per la posa in opera
Le trincee drenanti sono tra le soluzioni più efficaci per la stabilizzazione di frane superficiali traslazionali e colamenti in terreni a grana fine, dove le pressioni interstiziali giocano un ruolo determinante.
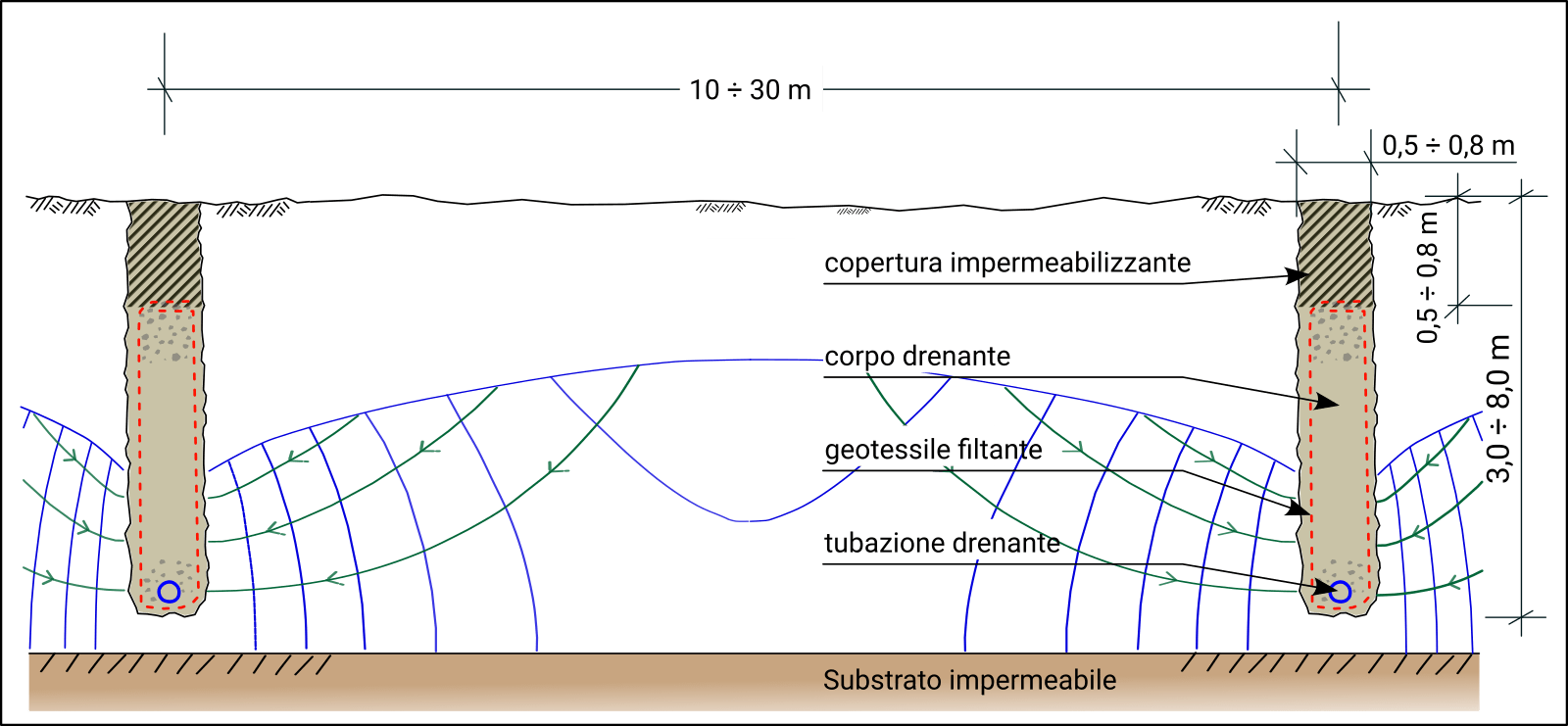
Figura 1 – Sezione trasversale tipologica di un sistema di trincee drenanti.
Profondità e Interasse
Lo scavo di una trincea drenante ha generalmente una larghezza compresa tra 50 e 80 cm, mentre la profondità ottimale di una trincea drenante si aggira tra 6 e 8 metri. Escavazioni fino a 30 metri sono possibili con tecniche avanzate, ma oltre una certa profondità, soluzioni come i pozzi drenanti possono risultare più vantaggiose.
L’interasse tra le trincee è determinato in base alle caratteristiche idrauliche e geotecniche del sito, indicativamente tra i 10 e 30 m. Una corretta spaziatura migliora la copertura drenante dell’area instabile, evitando accumuli localizzati di pressione interstiziale.
Orientamento
Le trincee drenanti dovrebbero essere allineate lungo la massima pendenza del versante, per ottimizzare il deflusso dell’acqua sotterranea e massimizzare l’effetto di riduzione delle pressioni interstiziali. Una disposizione trasversale, al contrario, può favorire l’accumulo idrico e aumentare il rischio di riattivazione del movimento franoso, soprattutto in presenza di infiltrazioni concentrate o di difetti esecutivi.
Nella pratica progettuale si adotta spesso uno schema a spina di pesce, in cui il collettore principale segue la linea di massima pendenza, mentre le trincee secondarie (le “spine”) attraversano trasversalmente il corpo di frana, disposte con pendenze differenziate per evitare il ristagno dell’acqua.
Dettagli costruttivi
Per migliorare la capacità di deflusso sul fondo delle trincee, si installano tubazioni forate di diametro generalmente compreso tra 160 e 200 mm. Queste possono essere protette con geotessili filtranti, con lo scopo di prevenire l’intasamento.
In corrispondenza delle trincee è utile predisporre cunette superficiali di raccolta, che svolgono una duplice funzione: individuare la posizione planimetrica dell’intervento realizzato e prevenire le infiltrazioni dirette all’interno del corpo drenante, contribuendo a migliorare la gestione delle acque superficiali.
Per mantenere l’efficienza del sistema nel tempo, si raccomanda l’installazione di pozzetti di ispezione, che consentono il monitoraggio periodico e l’eventuale lavaggio delle tubazioni mediante getti d’acqua in pressione.
Materiali Drenanti e Filtri
La scelta del materiale drenante è fondamentale per garantire la funzionalità a lungo termine delle trincee. È necessario utilizzare materiali a granulometria controllata, con l’eventuale integrazione di filtri geotessili per prevenire fenomeni di intasamento e garantire la continuità della capacità drenante nel tempo. Negli ultimi anni, sono stati sviluppati sistemi prefabbricati per la realizzazione delle trincee drenanti, basati su strutture modulari e materiali leggeri, che semplificano l’installazione. Un esempio di questi elementi prefabbricati è disponibile qui.
Tuttavia, la durabilità di questi sistemi e la scelta del materiale filtrante ottimale sono ancora oggetto di ricerca nell’ambito della comunità scientifica internazionale. I test sperimentali su materiali innovativi stanno contribuendo a migliorare l’affidabilità e l’efficienza di queste soluzioni nel tempo [3].
Stabilità del Pendio ed Efficienza Idraulica
Per comprendere il ruolo dell’efficienza idraulica nella stabilizzazione dei pendii, è utile analizzare come le pressioni interstiziali influenzino il coefficiente di sicurezza. In condizioni semplificate — riferite a un pendio indefinito, omogeneo e soggetto a filtrazione stazionaria monodimensionale parallela al piano campagna (Figura 2) — il coefficiente di sicurezza \( F \) può essere espresso come:
$$
F = \frac{c’ + (\sigma_\beta – u_0) \tan \varphi’}{\tau_\beta}
$$
dove:
- \( c’\): coesione drenata del terreno
- \( \varphi’\): angolo di attrito efficace
- \( \sigma_\beta \), \( u_0 \),\( \tau_\beta \): rispettivamente tensione normale, pressione interstiziale e tensione tangenziale sul piano di scorrimento. Queste grandezze possono essere espresse in funzione della geometria del pendio e delle proprietà fisiche del terreno:
$$ \tau_\beta = \gamma Z \cos \beta \sin \beta\,,\quad $$
$$ \sigma_\beta = \gamma Z \cos^2 \beta\,, \quad$$
$$ u_0 = \gamma_w Z_w \cos^2 \beta $$
dove:
- \( \gamma \): peso specifico del terreno
- \( \gamma_w \): peso specifico dell’acqua
- \( Z \): profondità del piano considerato
- \( Z_w=Z-d_w \): altezza della falda
- \(d_w\): profondità della falda
- \( \beta \): inclinazione del pendio
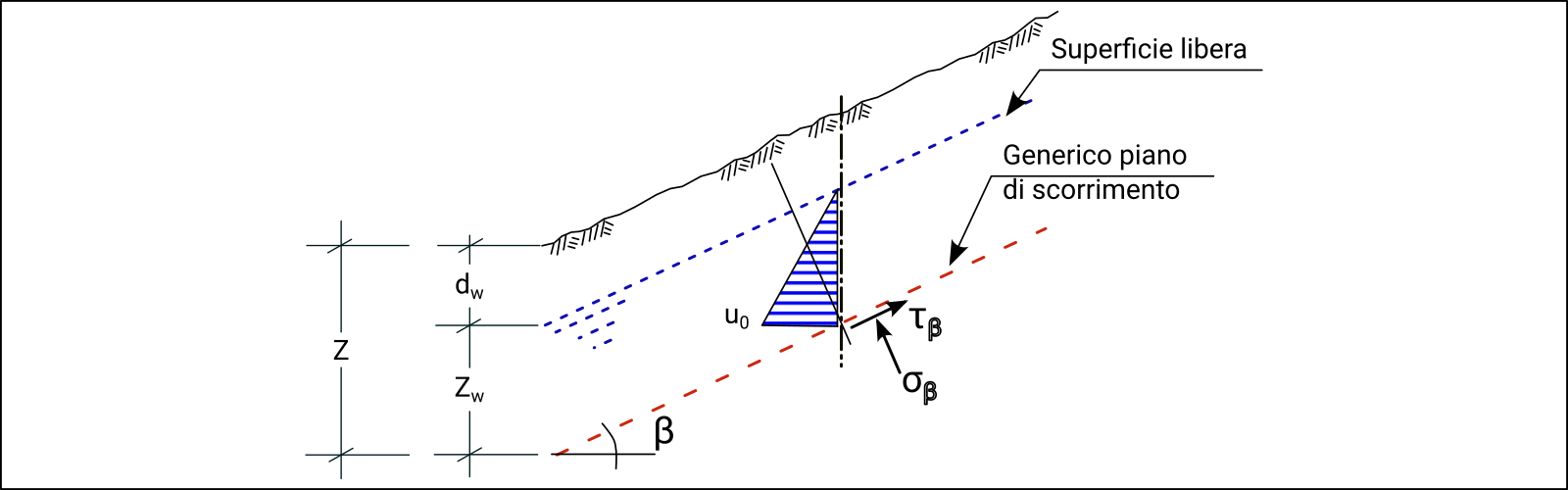
Figura 2 – Schema di pendio indefinito.
Il coefficiente di sicurezza può essere scomposto in tre termini distinti, ciascuno rappresentativo di una diversa componente della resistenza allo scorrimento:
$$F_{S1} = \frac{c’}{\tau_\beta}\,, \quad$$
$$F_{S2} = \frac{\sigma_\beta \tan \varphi’}{\tau_\beta}\,,\quad$$
$$ F_{S3} = -\frac{u_0 \tan \varphi’}{\tau_\beta} $$
dove:
- \( F_{S1} \): contributo coesivo
- \( F_{S2} \): contributo dovuto all’attrito efficace
- \( F_{S3} \): contributo destabilizzante associato alle pressioni interstiziali
Il drenaggio agisce direttamente sul termine destabilizzante \( F_{S3} \), riducendo la pressione interstiziale \( u_0 \) e determinando un incremento del coefficiente di sicurezza:
$$
\Delta F(t) = -\frac{\Delta u(t) \tan \varphi’}{\tau_\beta}
$$
dove \(\Delta u(t) = u(t) – u_0 \) rappresenta la variazione della pressione interstiziale nel tempo, con \(u(t)\) pressione al tempo (\(t\)), ed \(u_0\) quella iniziale. Il valore massimo ottenibile, in corrispondenza della completa dissipazione della pressione interstiziale (\( u (t) \to 0\)), è:
$$
\Delta F_{\text{max}} = \frac{u_0 \tan \varphi’}{\tau_\beta}
$$
Efficienza idraulica puntuale
Per descrivere l’evoluzione della pressione interstiziale nel tempo, si introduce l’efficienza idraulica puntuale:
$$
E(t) = \frac{u_0 – u(t)}{u_0}
$$
Per definizione, l’efficienza idraulica può essere calcolata anche come rapporto tra \( \Delta F(t)\) e \( \Delta F_{\text{max}} \):
$$
E(t) = \frac{\Delta F(t)}{\Delta F_{\text{max}}}
= \frac{u_0 – u(t)}{u_0}\,.
$$ da cui:
$$
\Delta F(t) = E(t) \cdot \Delta F_{\text{max}}\,.
$$ Quest’ultima equazione consente di interpretare l’efficienza idraulica come un indicatore diretto dell’incremento di stabilità locale, in funzione del tempo.
Efficienza idraulica media
La massima efficienza si osserva nei pressi della trincea, dove il gradiente di pressione è maggiore; essa diminuisce progressivamente con la distanza dalla sorgente di drenaggio (Figura 3). Per rappresentare l’efficacia complessiva del sistema, si introduce l’efficienza idraulica media \( E_{\text{med}}(t)\), definita come media spaziale dell’efficienza puntuale sulla superficie di scorrimento:
$$
E_{\text{med}}(t) = \frac{1}{S} \int_S E(t) \, ds
$$
dove ( \(S\) ) è la lunghezza del tratto drenato. Applicando la stessa logica vista in precedenza, si ottiene:
$$
\Delta F_{\text{med}}(t) = E_{\text{med}}(t) \cdot \Delta F_{\text{max}}
$$
Questa relazione consente di valutare in modo sintetico ed efficace l’incremento complessivo del coefficiente di sicurezza associato a un intervento di drenaggio.
Un sistema di drenaggio ben progettato massimizza l’efficienza idraulica media e, di conseguenza, l’incremento del coefficiente di sicurezza. La valutazione dell’efficienza può essere condotta tramite modelli numerici, oppure stimata mediante l’utilizzo di abachi ricavati da simulazioni consolidate e disponibili in letteratura tecnica.
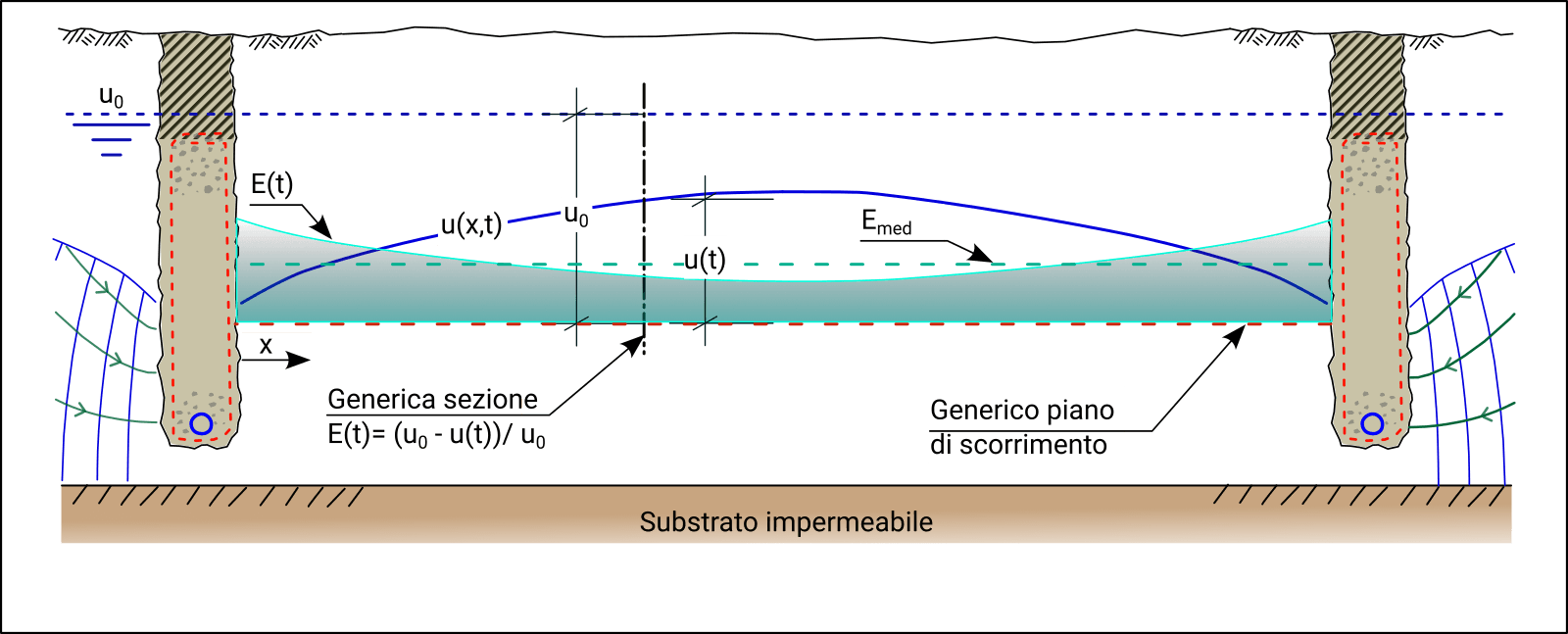
Figura 3 – Efficienza idraulica puntuale ed efficienza idraulica media.
Abachi per il Dimensionamento delle Trincee Drenanti
Nel paragrafo seguente si riportano i risultati di simulazioni numeriche semplificate che hanno permesso di costruire abachi utili per il dimensionamento preliminare dei sistemi drenanti. L’efficienza idraulica di un sistema di trincee drenanti può essere valutata a partire da simulazioni numeriche condotte in condizioni semplificate, basate su uno schema geometrico standard (Figura 4), dove:
- le trincee hanno sezione rettangolare, con larghezza \( B \) e profondità \( H_0 \);
- sono parallele e disposte secondo le linee di massima pendenza del pendio;
- il loro sviluppo longitudinale \( L \) è molto maggiore dell’interasse \(S\), il che consente di adottare un’analisi bidimensionale;
- il piano campagna è orizzontale nella direzione trasversale rispetto al pendio, mentre lungo la direzione longitudinale, il pendio assume un’inclinazione uniforme;
- le condizioni iniziali sono idrostatiche, con la falda che coincide con il piano campagna;
- il terreno è omogeneo, isotropo e saturo, limitato inferiormente da una formazione impermeabile posta a profondità \( H = n H_0\).
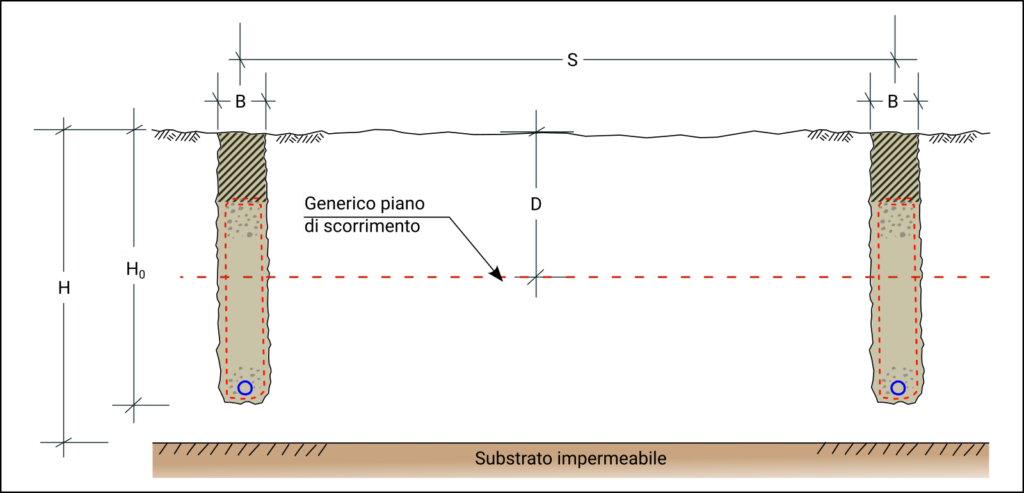
Figura 4 – Schema geometrico di riferimento per il dimensionamento delle trincee drenanti.
I risultati delle simulazioni sono stati normalizzati e riportati in abachi che correlano i principali parametri geometrici adimensionali:
- \( S/H_0 \) — interasse normalizzato (da \(0.5\) a \(6\));
- \( B/H_0 = 0.16 \) — larghezza normalizzata. Questo parametro è assunto costante poiché, nella pratica, la larghezza delle trincee risulta generalmente proporzionale alla profondità dello scavo. Inoltre, è stato dimostrato che il rapporto \( B/H_0 \) ha un’influenza trascurabile sui risultati finali.
- \( n=H/H_0 \), con \(n = 1, 1.5, 2.5\) e \(4.0\). Per \(n\geq 2.5\) i risultati non variano sensibilmente.
L’efficienza idraulica è stata valutata su piani paralleli al pendio posti a profondità normalizzate:
- \( d=D/H_0 \) per \(d =0.5, 1.0, 1.5\) e \(2.0\)
Per casi di anisotropia nella permeabilità del terreno, è possibile adottare un interasse equivalente fittizio \( S^* \) definito da:
$$
S^* = S \cdot \sqrt{\frac{k_v}{k_h}}
$$
dove:
- \( k_v \): permeabilità verticale;
- \( k_h \): permeabilità orizzontale.
Evoluzione Temporale dell’Efficienza Idraulica
L’evoluzione nel tempo dell’efficienza è stata studiata tramite il fattore di tempo adimensionale \(T\), definito come:
$$
T = \frac{k_v \cdot \gamma_w \cdot H_0^2}{E’ \cdot 2(1 + \nu’)(1 – 2\nu’)} \cdot t
$$
dove:
- \( k_v \): permeabilità verticale del terreno;
- \( \gamma_w \): peso specifico dell’acqua;
- \( E’ \): modulo elastico tangente;
- \( \nu’ \): coefficiente di Poisson del terreno;
- \( t\): tempo.
Portata drenata
Nella progettazione di un sistema di drenaggio è fondamentale valutare la portata che il sistema è in grado di smaltire, in funzione delle caratteristiche idrauliche del terreno e della geometria adottata. Una stima adeguata della portata drenata per unità di lunghezza, \(Q\), consente di verificare se il dispositivo sia effettivamente in grado di intercettare e convogliare i volumi idrici attesi, evitando accumuli e sovraccarichi.
A partire dal coefficiente di permeabilità orizzontale del terreno \(k_h\), è possibile stimare \(Q\) attraverso l’impiego di diagrammi empirici che mettono in relazione la configurazione geometrica del sistema con la sua capacità drenante [2]. Nel caso di trincee che raggiungono il substrato impermeabile, la portata drenata può essere ricondotta a un fattore di portata adimensionale:
$$
q = \frac{Q}{D \cdot k_h}\sqrt{\frac{k_v}{k_h}}
$$
in funzione del parametro geometrico:
$$
s = \frac{S^*}{2\cdot D}
$$
Questa formulazione, pur essendo stata derivata per configurazioni che raggiungono lo strato impermeabile alla base (\(n=1\)), fornisce stime affidabili anche in per \(n>1\). In prima approssimazione, infatti, il moto di filtrazione al di sotto del corpo drenante può essere trascurato nella determinazione delle portate drenate.
Considerazioni Progettuali
Dai risultati ottenuti, emergono le seguenti osservazioni fondamentali:
- L’efficienza idraulica media decresce all’aumentare del rapporto \( S/H_0 \);
- È più elevata nei piani che attraversano le trincee rispetto a quelli situati al di sotto;
- Per \( D/H_0 \) compreso tra 1.5 e 2.0 (zone sotto le trincee), l’efficienza è circa la metà di quella per \( D/H_0 = 0.5 \div 1.0 \);
- Per \( n > 1.5 \), la profondità del substrato impermeabile non influisce sensibilmente sull’efficienza nei piani superiori;
- I tempi per raggiungere il regime aumentano con \( S/H_0 \), soprattutto nei piani profondi.
📌 Raccomandazione progettuale:
Per massimizzare l’efficienza idraulica e ridurre i tempi di risposta del sistema, è consigliabile realizzare trincee che raggiungano o superino la superficie di scorrimento e limitare l’interasse tra di esse secondo le condizioni geotecniche del sito.
Strumenti per il Dimensionamento
Per chi desidera approfondire gli aspetti pratici legati al dimensionamento di massima delle trincee drenanti, è disponibile un notebook Jupyter accompagnato da una libreria Python dedicata, che implementa le principali relazioni presentate in questo articolo.
📁 Il codice è liberamente consultabile e scaricabile al seguente link:
👉 https://github.com/FraJoMen/franciscojmendez_Risorse/tree/main/articolo_01_trincee_drenanti
Il repository contiene:
- funzioni di calcolo dell’efficienza idraulica;
- grafici basati sugli abachi di letteratura;
- esempi d’uso.
Contributi, segnalazioni o suggerimenti sono benvenuti!
Bibliografia e Approfondimenti
- Desideri A., Miliziano S., Rampello S. (1997). Drenaggi a gravità per la stabilizzazione dei pendii. Argomenti di Ingegneria Geotecnica, Hevelius Edizioni, Benevento. Link al documento PDF.
- Ordine dei Geologi della Sardegna (s.d.). La progettazione delle trincee drenanti per la stabilizzazione dei pendii. Miscellanea Sarda. Link al documento PDF.
- Elzoghby M.M., Jia Z., Luo W. (2021). Experimental study on the hydraulic performance of nonwoven geotextile as subsurface drain filter in a silty loam area. Journal of Rock Mechanics and Geotechnical Engineering, 13(6), 1405–1418. Link all’articolo.
Per ulteriori approfondimenti sulla progettazione, il dimensionamento e la verifica dell’efficienza dei sistemi drenanti, si segnalano i seguenti riferimenti:
- Washington State Department of Transportation (2009).
Design Guidance for Horizontal Drains Used for Slope Stabilization.
WSDOT Research Report WA-RD 787.1
Documento completo che affronta il tema del drenaggio orizzontale per la stabilizzazione dei pendii, con linee guida progettuali, casi studio e risultati sperimentali. - Corsi e seminari
Il tema del dimensionamento delle trincee drenanti è oggetto di costanti approfondimenti tecnici da parte del Prof. Maurizio Ponte, che organizza e partecipa regolarmente a seminari e incontri di aggiornamento professionale:🔗 Profilo docente – Prof. Maurizio Ponte.
Tra i contributi recenti si segnalano:
– Progettazione e verifica delle trincee drenanti – Ordine dei Geologi delle Marche (2023)
– Le trincee drenanti nei versanti in frana – Seminario ARRIGO GABBIONI ITALIA (2024) - GeoStru WebApp – Trincee drenanti
Applicazione interattiva per il calcolo dell’efficienza idraulica e la valutazione progettuale
https://geoapp.geostru.eu/app/trincee-drenanti/
Uno strumento utile per effettuare simulazioni basato sugli abachi proposti da Desideri et al. [1].

